El siguiente enlace los llevará al documento Nº4 de Provincia de Buenos Aires "ORIENTACIONES DIDÁCTICAS PARA LA ENSEÑANZA DE LA MULTIPLICACIÓN EN LOS TRES CICLOS DE LA EGB " http://abc.gov.ar/lainstitucion/sistemaeducativo/educprimaria/areascurriculares/matematica/multiplicacion.pdf
miércoles, 2 de noviembre de 2011
LA ENSEÑANZA DE LA MULTIPLICACIÓN
El siguiente enlace los llevará al documento Nº4 de Provincia de Buenos Aires "ORIENTACIONES DIDÁCTICAS PARA LA ENSEÑANZA DE LA MULTIPLICACIÓN EN LOS TRES CICLOS DE LA EGB " http://abc.gov.ar/lainstitucion/sistemaeducativo/educprimaria/areascurriculares/matematica/multiplicacion.pdf
lunes, 31 de octubre de 2011
LA ENSEÑANZA DE LA DIVISIÓN
ORIENTACIONES DIDÁCTICAS
EL SIGUIENTE ENLACE LOS LLEVARÁ A UN DOCUMENTO DEL GOBIERNO DE LA PROVINCIA DE BUENOS AIRES : "ORIENTACIONES DIDÁCTICAS PARA LA ENSEÑANZA DE LA DIVISIÓN"
EL MISMO VA MOSTRANDO COMO TRABAJAR LA DIVISIÓN DESDE PRIMER GRADO HASTA EL TERCER CICLO Y DA EJEMPLOS DE LOS POSIBLES PROCEDIMIENTOS QUE UTILIZAN LOS NIÑOS AL RESOLVER LAS SITUACIONES PROPUESTAS.
CONSTRUCCIÓN DEL SENTIDO DE LA DIVISIÓN
EL MATERIAL ESTÁ ORIENTADO PARA TERCER GRADO, ES UNA PUBLICACIÓN DE UNICEF. PRESENTA UNA SECUENCIA DE ACTIVIDADES EN TORNO AL TRABAJO AÚLICO EN TERCER GRADO.
PARA ENSEÑAR LA DIVISIÓN LAS AUTORAS: PIERINA LANZA E IRMA SCHEY PRESENTAN DE UNA MANERA CLARA SUGERENCIAS Y TIPOS DE PROBLEMAS QUE PERMITE AL ALUMNO COMPRENDER LOS DIFERENTES SIGNIFICADOS QUE INVOLUCRA LA DIVISIÓN.
"TODOS PUEDEN APRENDER MATEMÁTICA " 3
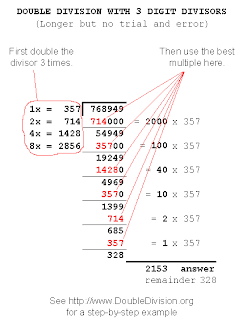
LAS SIGUIENTES IMÁGENES NOS PUEDEN IR GUIANDO CÓMO ACORTAR LA DIVISIÓN
DESPUÉS DE HABER APRENDIDO ESTIMAR EL ORDEN DEL COCIENTE IR BUSCANDO CUÁNTAS VECES SE PUEDE QUITAR ESA POTENCIA DE DIEZ.
EL SIGUIENTE ENLACE LOS LLEVARÁ A UN DOCUMENTO DEL GOBIERNO DE LA PROVINCIA DE BUENOS AIRES : "ORIENTACIONES DIDÁCTICAS PARA LA ENSEÑANZA DE LA DIVISIÓN"
EL MISMO VA MOSTRANDO COMO TRABAJAR LA DIVISIÓN DESDE PRIMER GRADO HASTA EL TERCER CICLO Y DA EJEMPLOS DE LOS POSIBLES PROCEDIMIENTOS QUE UTILIZAN LOS NIÑOS AL RESOLVER LAS SITUACIONES PROPUESTAS.
CONSTRUCCIÓN DEL SENTIDO DE LA DIVISIÓN
EL MATERIAL ESTÁ ORIENTADO PARA TERCER GRADO, ES UNA PUBLICACIÓN DE UNICEF. PRESENTA UNA SECUENCIA DE ACTIVIDADES EN TORNO AL TRABAJO AÚLICO EN TERCER GRADO.PARA ENSEÑAR LA DIVISIÓN LAS AUTORAS: PIERINA LANZA E IRMA SCHEY PRESENTAN DE UNA MANERA CLARA SUGERENCIAS Y TIPOS DE PROBLEMAS QUE PERMITE AL ALUMNO COMPRENDER LOS DIFERENTES SIGNIFICADOS QUE INVOLUCRA LA DIVISIÓN.
"TODOS PUEDEN APRENDER MATEMÁTICA " 3
LAS SIGUIENTES IMÁGENES NOS PUEDEN IR GUIANDO CÓMO ACORTAR LA DIVISIÓN
DESPUÉS DE HABER APRENDIDO ESTIMAR EL ORDEN DEL COCIENTE IR BUSCANDO CUÁNTAS VECES SE PUEDE QUITAR ESA POTENCIA DE DIEZ.
martes, 18 de octubre de 2011
CUADERNOS PARA EL AULA
Les dejo los enlaces para lo que necesiten buscar en los Cuadernos para el Aula
PRIMER GRADO
Matemática – 1,3 Mb
SEGUNDO GRADO
Matemática – 4,5 Mb
TERCER GRADO
Matemática – 2,6 Mb
CUARTO GRADO
Matemática – 5,9 Mb
QUINTO GRADO
Matemática – 6,0 Mb
SEXTO GRADO
Matemática – 4,5 Mb
PRIMER GRADO
Matemática – 1,3 Mb SEGUNDO GRADO
Matemática – 4,5 Mb
TERCER GRADO
Matemática – 2,6 Mb
CUARTO GRADO
Matemática – 5,9 Mb
QUINTO GRADO
Matemática – 6,0 Mb
SEXTO GRADO
Matemática – 4,5 Mb
LA ENSEÑANZA DE LAS OPERACIONES EN EL CAMPO ADITIVO
El campo aditivo involucra las operaciones adición y sustracción. Uno de los indicadores para poder determinar si el alumno domina un contenido matemático es la capacidad de reconocerlo como herramienta de resolución en el conjunto de problemas con diferentes significados que éste resuelve.
Vergnaud se basa en tres tipologías que va luego combinando: composición de medidas, transformaciones( positivas y negativas) y estados relativos. La variación del lugar de la incógnita amplía las posibilidades de trabajar significaciones diferentes.
Los niños en primer grado deben hacer la evolución del conteo hacia el cálculo mental reflexivo de adiciones y sustracciones. Estos problemas los niños los resolverán dibujando, haciendo íconos o con material concreto y luego contando o sobrecontando. Podemos indicar que el niño está calculando cuando no necesita contar ni sobrecontar sino establecer relaciones numéricas para dar la solución. La idea es trabajar descomposiciones aditivas y composiciones en torno al cinco y al diez para simplificar el cálculo.
Para hacer la transición del nivel Inicial al Primario podemos ver la conferencia de Irma Fuenlabrada sobre la Enseñanza de la Matemática en el Nivel Inicial
El siguiente material de Capacitación Docente de la Provincia de Mendoza les permitirá reflexionar sobre el tratamiento del número, sistema de numeración y adición y sustracción en el primer ciclo.
Para segundo grado:
2°grado_ definitivo
Para tercer Grado
TPA Primera capacitacióm 3º grado primera parte
TPA Primera capacitacióm 3º grado segunda parte
Vergnaud se basa en tres tipologías que va luego combinando: composición de medidas, transformaciones( positivas y negativas) y estados relativos. La variación del lugar de la incógnita amplía las posibilidades de trabajar significaciones diferentes.
Los niños en primer grado deben hacer la evolución del conteo hacia el cálculo mental reflexivo de adiciones y sustracciones. Estos problemas los niños los resolverán dibujando, haciendo íconos o con material concreto y luego contando o sobrecontando. Podemos indicar que el niño está calculando cuando no necesita contar ni sobrecontar sino establecer relaciones numéricas para dar la solución. La idea es trabajar descomposiciones aditivas y composiciones en torno al cinco y al diez para simplificar el cálculo.
Para hacer la transición del nivel Inicial al Primario podemos ver la conferencia de Irma Fuenlabrada sobre la Enseñanza de la Matemática en el Nivel Inicial
El siguiente material de Capacitación Docente de la Provincia de Mendoza les permitirá reflexionar sobre el tratamiento del número, sistema de numeración y adición y sustracción en el primer ciclo.
Para segundo grado:
2°grado_ definitivoPara tercer Grado
TPA Primera capacitacióm 3º grado primera parte
TPA Primera capacitacióm 3º grado segunda parte
martes, 13 de septiembre de 2011
LA BANDA NUMÉRICA DE PRIMER GRADO
La Banda numérica es un portador numérico que permite a los alumnos:
Ver en: http://des.mza.infd.edu.ar/sitio/upload/1_jornada_2_grado_09.pdf
El rol de maestro no consiste en enseñar los números uno tras otro, sino proponer a los niños situaciones que les permitan conocerlos y descubrir las regularidades de nuestro sistema.
Algunas situaciones adecuadas para este trabajo son las siguientes:
EL JUEGO DE LA LOTERÍA
En "Mariamatica" podemos acceder a la secuencia didáctica del juego de la lotería que con el auxilio de este recurso didáctico permite descubrir las regularidades del sistema de numeración escrito y establecer las relaciones que este tiene con el sistema de numeración oral.
http://mariamatica.blogspot.com/2011/02/la-loteria-para-aprender-los-numeros.html
EL JUEGO DEL CASTILLO:
Extraído textualmente de: http://abc.gov.ar/lainstitucion/sistemaeducativo/educprimaria/areascurriculares/matematica/algunasreflexionesentornoalaensenianzadelamatematicaen1ciclo.pdf donde podemos leer la secuencia didáctica en la que se incluye este juego cuyos objetivos son:
* El reconocimiento de la escritura en cifras de los números.
* La localización de esas escrituras en una tabla de números presentados en filas de diez.
* La toma de conciencia del diferente rol que juega cada cifra en la escritura de un número.
* El aprendizaje y la utilización del nombre de la decenas.
* La búsqueda de regularidades del Sistema de Numeración Decimal
* La utilización de procedimientos para encontrar resultados.
El juego inicial;
El tablero se presenta a los niños como un "castillo" que tiene 100 cuartos. Como son tantos
cuartos, para poder identificarlos están numerados. Se les cuenta a los niños que algunos números van a
estar tapados por un cartoncito y que la actividad consiste en decir qué número es el que está escondido.
Se puede hacer una presentación colectiva de la actividad en un tablero en el pizarrón, con
algunos números tapados y pedir a los niños que señalen un cuarto y nombren el número correspondiente.
Luego se destapa y se corrobora.
A continuación se organiza la clase en grupos de 5 ó 6 niños, cada uno con un tablero individual y
tantos números tapados como jugadores (o el doble si se quiere que jueguen dos veces cada uno). Puede
otorgarse puntaje (2, 3 o 4 puntos, en el reverso del cartoncito), que se obtiene cuando se dice el número
correcto.
En su turno, cada jugador elige el cuarto que va a identificar, dice el número y, si es correcto, gana
esos puntos.
Un posible castillo:
0 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19
20 21 22 23 24 25 26 27 28 29
30 31 32 33 34 35 36 37 38 39
40 41 42 43 44 45 46 47 48 49
50 51 52 53 54 55 56 57 58 59
60 61 62 63 64 65 66 67 68 69
70 71 72 73 74 75 76 77 78 79
80 81 82 83 84 85 86 87 88 89
90 91 92 93 94 95 96 97 98 99
También podemos acceder a actividades con el "Juego del Castillo" y actividades para calcular utilizando la banda numérica de la capacitación de la misma provincia en:
http://des.mza.infd.edu.ar/sitio/upload/1_Sec_2_grado_2009_def.pdf
CALCUDEDO:
Es muy interesante la propuesta didáctica calcudedo publicada por 12ntes en http://www.12ntes.com/?page_id=39
También en el documento citado anteriormente de Provincia de Buenos Aires "Algunas reflexiones en torno a la Enseñanza de la Matemática en el Primer Ciclo" podemos ver cómo utilizar la banda numérica para calcular
http://abc.gov.ar/lainstitucion/sistemaeducativo/educprimaria/areascurriculares/matematica/algunasreflexionesentornoalaensenianzadelamatematicaen1ciclo.pdf
ACTIVIDAD GRUPAL_
LA EXPOSICIÓN PARA SOCIALIZAR LAS PRODUCCIONES CON TODO EL CURSO EL VIERNES 25 DE SEPTIEMBRE.
- Establecer relaciones entre la serie oral y escrita. En ella se apoyan los niños para leer y escribir números.Por ejemplo si un niño no sabe leer el 17, que podría ser el numero dibujado en una carta de un juego o bien el número que esta escrito en la bolilla que tiene que leer en el juego de la lotería....entonces recitando la serie sobre la banda y asignando a cada símbolo una palabra número, partiendo desde el uno, podrán saber que el numero que tienen en sus manos es el diecisiete. Análogamente cuando quiera escribir el "diecisiete" o reconocerlo procederá a recitar la serie hasta encontrar el símbolo que biunivocamente corresponde a la palabra "diecisiete".
- Descubrir regularidades en la serie escrita, ya que las columnas terminan con la misma cifra y las filas comienzan con la misma cifra mostrando las familias de los veinti.., treinti.., etc.
- Realizar cálculos en el campo aditivos desplazándose sobre la banda. Desplazarse hacia la derecha en una misma fila implica sumar y si lo hacemos hacia la izquierda es restar. Si subimos un lugar en la misma columna el número disminuye en 10 y si bajamos se agregan 10. También se puede trabajar en el campo multiplicativo con escalas del 2, 4, 5, etc. , pintando los números y anticipando resultados de tablas.
Ver en: http://des.mza.infd.edu.ar/sitio/upload/1_jornada_2_grado_09.pdf
El rol de maestro no consiste en enseñar los números uno tras otro, sino proponer a los niños situaciones que les permitan conocerlos y descubrir las regularidades de nuestro sistema.
Algunas situaciones adecuadas para este trabajo son las siguientes:
EL JUEGO DE LA LOTERÍA
En "Mariamatica" podemos acceder a la secuencia didáctica del juego de la lotería que con el auxilio de este recurso didáctico permite descubrir las regularidades del sistema de numeración escrito y establecer las relaciones que este tiene con el sistema de numeración oral.
http://mariamatica.blogspot.com/2011/02/la-loteria-para-aprender-los-numeros.html
EL JUEGO DEL CASTILLO:
Extraído textualmente de: http://abc.gov.ar/lainstitucion/sistemaeducativo/educprimaria/areascurriculares/matematica/algunasreflexionesentornoalaensenianzadelamatematicaen1ciclo.pdf donde podemos leer la secuencia didáctica en la que se incluye este juego cuyos objetivos son:
* El reconocimiento de la escritura en cifras de los números.
* La localización de esas escrituras en una tabla de números presentados en filas de diez.
* La toma de conciencia del diferente rol que juega cada cifra en la escritura de un número.
* El aprendizaje y la utilización del nombre de la decenas.
* La búsqueda de regularidades del Sistema de Numeración Decimal
* La utilización de procedimientos para encontrar resultados.
El juego inicial;
El tablero se presenta a los niños como un "castillo" que tiene 100 cuartos. Como son tantos
cuartos, para poder identificarlos están numerados. Se les cuenta a los niños que algunos números van a
estar tapados por un cartoncito y que la actividad consiste en decir qué número es el que está escondido.
Se puede hacer una presentación colectiva de la actividad en un tablero en el pizarrón, con
algunos números tapados y pedir a los niños que señalen un cuarto y nombren el número correspondiente.
Luego se destapa y se corrobora.
A continuación se organiza la clase en grupos de 5 ó 6 niños, cada uno con un tablero individual y
tantos números tapados como jugadores (o el doble si se quiere que jueguen dos veces cada uno). Puede
otorgarse puntaje (2, 3 o 4 puntos, en el reverso del cartoncito), que se obtiene cuando se dice el número
correcto.
En su turno, cada jugador elige el cuarto que va a identificar, dice el número y, si es correcto, gana
esos puntos.
Un posible castillo:
0 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15 16 17 18 19
20 21 22 23 24 25 26 27 28 29
30 31 32 33 34 35 36 37 38 39
40 41 42 43 44 45 46 47 48 49
50 51 52 53 54 55 56 57 58 59
60 61 62 63 64 65 66 67 68 69
70 71 72 73 74 75 76 77 78 79
80 81 82 83 84 85 86 87 88 89
90 91 92 93 94 95 96 97 98 99
También podemos acceder a actividades con el "Juego del Castillo" y actividades para calcular utilizando la banda numérica de la capacitación de la misma provincia en:
http://des.mza.infd.edu.ar/sitio/upload/1_Sec_2_grado_2009_def.pdf
CALCUDEDO:
Es muy interesante la propuesta didáctica calcudedo publicada por 12ntes en http://www.12ntes.com/?page_id=39
También en el documento citado anteriormente de Provincia de Buenos Aires "Algunas reflexiones en torno a la Enseñanza de la Matemática en el Primer Ciclo" podemos ver cómo utilizar la banda numérica para calcular
http://abc.gov.ar/lainstitucion/sistemaeducativo/educprimaria/areascurriculares/matematica/algunasreflexionesentornoalaensenianzadelamatematicaen1ciclo.pdf
ACTIVIDAD GRUPAL_
- FORMAR TRES GRUPOS DE TRABAJO.
- CADA GRUPO ELEGIR UNA SECUENCIA: LA LOTERÍA, EL CASTILLO O CALCUDEDO,
- DETERMINAR OBJETIVOS,CANTIDAD DE CLASES QUE DEDICARÍAN, CONTENIDOS DE CADA CLASE Y ACTIVIDADES A REALIZAR, MODO DE UTILIZACIÓN DE LA BANDA NUMÉRICA.
- ORGANIZAR LA SECUENCIA EN UN POWER POINT
LA EXPOSICIÓN PARA SOCIALIZAR LAS PRODUCCIONES CON TODO EL CURSO EL VIERNES 25 DE SEPTIEMBRE.
sábado, 10 de septiembre de 2011
TRABAJO PRÁCTICO: ANÁLISIS DE CLASES
Instituto Carlos Alberto Leguizamón
Unidad Curricular: Didáctica de la Matemática I
Profesora: Silvia Signorile
Objetivos:Analizar propuestas de enseñanza reconociendo los supuestos teóricos en que se basan.
· Analizar el rol del docente según la metodología de enseñanza adoptada.
· Reelaborar y diseñar situaciones didácticas para la enseñanza de la divisibilidad en el segundo ciclo de enseñanza Primaria.
Criterios de evaluación:1. Claridad y coherencia en respuestas y argumentaciones.
2. Aplicación los conceptos teóricos específicos y referencia a los autores abordados en el análisis de clases desarrolladas y planificación de las mismas a desarrollar.
3. Creatividad en la elaboración de propuestas encuadradas en el marco teórico analizado.
ANÁLISIS DE CLASES:
Desarrollo de clases de divisibilidad Fuente: http://didacticaymatematica.idoneos.com/index.php/La_DivisibilidadSITUACIÓN PROBLEMÁTICA:
Un cartel tiene 4 luces de colores Amarillo, Verde; Rojo; Blanco.Se van encendiendo, por minuto. El primer minuto, la luz amarilla, el segundo minuto la verde, el tercer minuto la roja y el cuarto minuto la blanca. El quinto minuto la amarilla, el sexto minuto la verde y así continua. ¿Cuál es el color de la luz en el minuto 7?. ¿Y en el minuto 18?. ¿Y en el 35?. ¿y en el minuto 100?, ¿Y en el 412?. ¿Y en el 2.000?
DESCRIPCIÓN DE MOMENTOS IMPORTANTES DE LA CLASE :
Para resolverlo algunos alumnos fueron escribiendo, debajo de los colores, los distintos números hasta encontrar la respuesta.
A--V--R--B
1--2--3--4
5--6--7--8
...........
17-18
En el minuto 7 la luz es de color rojo y en el 18 es de color verde.
Al llegar al número 415 uno de los alumnos argumenta:
A1-Yo pensé que 400 es 4 veces 100, entonces es blanca. A partir de ahí conté 15 y llegué a rojo.
Se propuso el número 815. A1-Es igual, rojo, porque 800 va a ser blanca, y a partir de allí, se cuenta. A2-Con el 2.000 también llegas a la luz blanca.
Se propuso el número 2.136 A3-Con 2.000 llegas a la blanca. Habría que contar 136 y ver cuál es la luz.
Se propone descomponer el número 2.136. 2136 = 2.100 + 36 Esto permite que se den cuenta que no necesitan contar con un número tan “grande” como 136.
A partir de aquí los alumnos comienzan a darse cuenta que, una estrategia económica es dividir por 4, el número.
La pregunta es:¿cómo darse cuenta mirando, si el número o no es múltiplo de 4 o cuál es el resto que se obtiene.
Los alumnos proponen:
A1 tienen que terminar en 4. (Semejante al reconocimiento de los múltiplos de 5).Se propone el número 14.
A2. tienen que terminar en 0. (Han probado con 400. 800, 2.000). Se propone el número 70 . Algunos sugieren que deben terminar en dos ceros. (observando los ejemplos dados)
Se proponen los números 436; 1.348; 2.024. Observan que también son múltiplos de 4
Se procede a decomponer los números: 436= 400+36 1.348= 1.300 + 48; 2.024= 2.000 +24
Se concluye que es necesario que las dos últimas cifras sean múltiplos de 4.
Puede observarse que los alumnos han podido "descubrir" cuando un número es múltiplo de 4 y elaborar ellos la regla.
1-Responda las siguientes preguntas fundamentando con el marco teórico correspondiente
· ¿ La metodología utilizada por el docente que implicancias tiene en cuanto al “Saber”, “aprendizaje” y la “enseñanza”?
· ¿Cuál es el modelo de contrato didáctico que predomina en la clase?
· El docente elige intencionalmente una situación didáctica para que el saber, es decir, el contenido a enseñar sea construido por el alumno al intentar resolver la situación planteada. El contenido que se quiere enseñar es la herramienta óptima para resolver ese problema. ¿Qué contenido quiere que los alumnos descubran?
· ¿Qué tipo de situación didáctica es: acción, formulación o validación?
· ¿En el relato se detallan todos los momentos de la clase o fases?.
· Determine algún momento en el relato de la clase donde el docente realiza una “devolución” para que el medio “sancione” al alumno. Explique ambos conceptos.
· ¿Cuál es la variable didáctica que propone el maestro y con que finalidad lo hace?
· El conocimiento que la docente quiere enseñar surge del análisis de regularidades. “¿Cuál es la regularidad que quiere que los alumnos descubran?”
2-Diseñe una situación didáctica para la enseñanza de divisibilidad en el segundo ciclo de Enseñanza Primaria utilizando el juego.
Contenidos :o Múltiplos y divisores
o mcm
o DCM
o Números primos y compuestos
lunes, 15 de agosto de 2011
Suscribirse a:
Entradas (Atom)